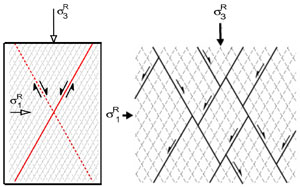
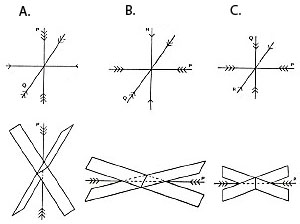
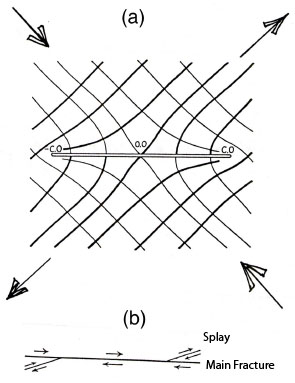
The Andersonian theory of faulting (Anderson 1951) is probably the earliest theory regarding the mechanism of faulting. It is based on the Coulomb failure criterion (sometimes referred to as the Mohr-Coulomb theory) which states that the shear stress necessary to cause brittle failure across a plane is equal to the cohesion of the material plus the internal friction coefficient times the normal stress across that plane. By this criterion, rocks will fail in two planes symmetric to the greatest compressive principle stress direction (Figure 1). The angle between the greatest compressive principle stress and the failure plane, sometimes referred to as the fault angle, is equal to the tangent of the friction coefficient. Using a laboratory-based friction value of 0.6, the corresponding angle is 30 degrees.

Figure 1. Illustration showing the two symmetric failure planes predicted by Anderson's theory of faulting. Sigma 3 is the most compressive while sigma 1 is the least compressive. The angle between the most compressive stress direction and the failure plane is 30 degrees assuming a friction coefficient of 0.6. From Aydin et al. (2003).

The Anderson model provides a framework to relate fault configuration and the sense of slip to Earth's surface and the principal stresses which drive the faulting. Earth's free surface is a principal plane by definition and the two other principal planes are orthogonal to it. Thus, there are three configurations of the principal stress direction with respect to Earth's free surface defining three types of faulting regimes: normal faults form when the greatest compression is perpendicular to Earth's surface (Figure 2A); reverse faults form when the greatest extension is perpendicular to Earth's surface (Figure 2B); strike-slip faults form when both are parallel to the Earth's surface (Figure 2C).

Figure 2. Three types of faults predicted by the Anderson theory of faulting. A. Normal fault with 60 degree dip angle produced by the most compressive stress perpendicular to Earth's surface. B. Reverse faults with 30 degree dip angle produced by the least compressive stress perpendicular to Earth's surface. C. Strike-slip faults with 90 degree dip angle produced by both the most compressive and least compressive principal stresses parallel to Earth\\'s surface. From Anderson (1951).

The theory summarized above offers explanations for the conjugate fault patterns observed in the field and predicts the stress directions. It has several important assumptions:

1. The blocks defining faults are rigid.

2. The ends of faults are left out or neglected.

3. Slip along a given fault is constant and is in the same direction.

4. The slip gradient is neglected.

5. Faults are generally straight and planar.

6. Fault intersection and interaction are not considered.

7. The model deals with frozen state devoid of fault initiation, propagation, and growth.

8. Unless there are planes of weakness in the two orientations defined above, every plane in these orientations are potential failure planes.

9. The model doesn't address the structure of the fault, like fault core and damage zone.

A less known part of Anderson's faulting theory deals with stress trajectories around a fracture following Inglis' concept of stress concentration around fractures. The fracture plane is under pure shear loading, two remote principal stresses are equal with opposite sign, inclined 45 and 135 degrees to the fracture. Anderson calculated the distribution of the principal stresses around such a fracture (Figure 3a) and also inferred the location, orientation, and slip sense of the secondary faults formed in such an environment (Figure 3b). This part of Anderson's work touches the fundamentals of faulting mechanisms, yet was never widely noticed.

Figure 3. (a) Stress trajectories around a fault. (b) Inferred location, orientation, as well as slip sense of splay secondary faults. From Anderson (1951).