Cataclastic deformation refers to a flow-like deformation of granular or crystalline materials produced by two micromechanical processes on the micro-scale: Grain fracture and pore collapse.

Grain fracturing (Figure 1) refers to the break of grains when the stress at a grain contact or grain contacts exceeds the strength of the grains or the fracture toughness (Gallagher, 1987; Du Bernard and Maerten, 2001). Grain fracturing leads to reduction of grain size (Figure 2 and Figure 3 (a,b)) and change of petrophysical properties of the aggregate (Figure 3(c,d)).

Figure 1. (a) Photo elastic experiments illustrating stress concentration at contacts of discs subjected to uniaxial compression. From Gallagher (1987). (b) Dynamic Element Modeling of stress localization in a grain subjected to uniaxial compression. From Du Bernard and Maerten (2001).

Figure 2. Photomicrographs of shear bands with grain fracturing and comminution. (a) Courtesy of Xavier Du Bernard and Peter Eichhubl.

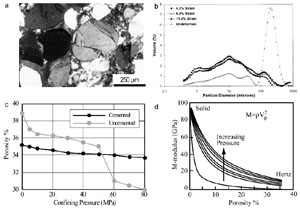Figure 3. (a) Image of initial grain fractures in sandstone. (b) Grain size distribution in shear bands with varying amounts of strain compared with undeformed sandstone (Mair et al., 2000). (c) Plots showing the relationship between porosity and confining pressure for cemented as well as non-cemented granular material (Dvorkin and Nur, 1996). (d) Dependence of M-modulus (the bulk density of aggregate times the square of P-wave velocity) on porosity for various effective pressures (Dvorkin and Nur, 1996).