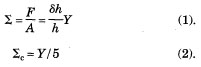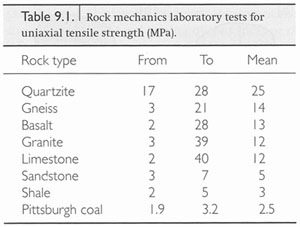
Strength measures how rocks resist force particularly at their break or failure. There are many ways of defining material strength. At the atomic scale, Marder and Fineberg (1996) estimated the strength of perfect solid from Young's modulus (Equation 1) with the assumption that the material fractures when the atoms move apart by a distance about 20% of their original spacing.

Equation 1. Equation of theorical strength of prefect solid on the atomic scale. (1) Take a block of material of height h, cross sectional area A, pulled by a force F, the block separates into halves when its atoms are pulled beyond the breaking point. The force needed to reach this goal is related to the stress, Sigma, and the Young's modulus through this relation. (2) The critical stress to make the atoms in the block move apart by 20% of their original spacing. From Marder and Fineberg (1996).

However, the actual strength of material is determined by the flaws because they act as stress concentrators. Generally, the actual strength is about two orders of magnitude smaller than the theoretical strength (Marder and Fineberg, 1996).

The actual strength of rock is also different under different loading conditions.

The uniaxial tensile strengths range over about one order of magnitude among rock types, and even among different samples of the same lithology. The tensile strengths for crystalline rocks can be as small as those for clastic sedimentary rocks, but typically they are somewhat greater. The laboratory specimens of rock have uniaxial tensile strengths that range from 2 to 40 MPa with a typical value of about 10 MPa. A data set for uniaxial tensile strengths is given in the table in Figure 1.

Figure 1. Rock mechanics laboratory tests for uniaxial tensile strength (MPa) for various rock types. From Pollard and Fletcher (2005).

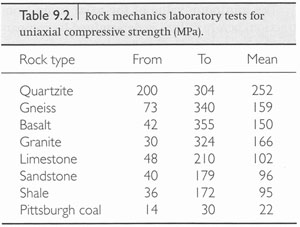
The uniaxial compressive strengths range over about one order of magnitude. Crystalline rocks tend to have greater compressive strengths than clastic sedimentary rocks, but some granites are weaker than some shale. Laboratory specimens of rocks have uniaxial compressive strengths that range from about 30 to 350 MPa with a typical value of about 150 MPa. A data set for uniaxial compressive strengths is given in the table in Figure 2.

Figure 2. Rock mechanics laboratory tests for uniaxial compressive strength (MPa) for vaious rock types. From Pollard and Fletcher (2005).

Comparing the uniaxial tensile and compressive strengths, we can see that typical laboratory samples are about one order of magnitude weaker in tension than in compression. Combined with stress inversion, this explains why faults aren't likely to form in pristine rocks before the rock fails in tension. This has profound implication for the development of brittle deformation in Earth's crust.