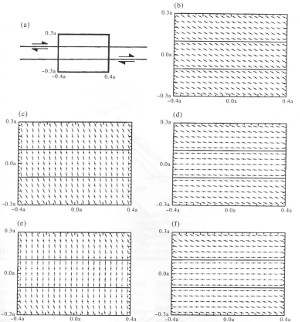
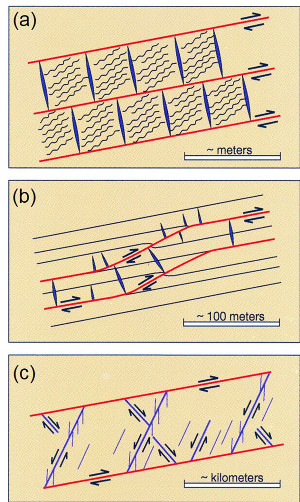
The simplest conceptual model for crustal scale thrust fault systems generally includes one primary set of thrust faults localized in horizontal or low-angle weak stratigraphic units (Boyer and Elliott in early 1980s and Suppe, 1985; and his co-workers, Dahlen et al., 1984). The latter is based on a faulting mechanisms and named the critical wedge theory to analyze primarily foreland-directed thrusting in terms of the strength of sedimentary rocks. Suppe (1985) also proposed thrust fault-related folding illustrated in other categories in this Knowledgebase.

An outcrop-scale study by Ohlmacher and Aydin (1997) employed a displacement discontinuity method to calculate the stress distribution associated with sub-parallel horizontal or low-angle slip planes shown in Figure 1(a). The diagrams in (b) through (f) summarize the maximum and minimum principal stress orientations as a function of the friction coefficients along the shear fractures and the orientation of the driving stresses. The conclusions were that the orientation of the maximum and minimum principal stresses vary from oblique to the shear fracture (b), to high-angle (c and e), and sub-parallel to the shear fractures (d and f).

Figure 1. Distribution of principal stresses (largest and smallest as represented longer and shorter tick marks, respectively) between sub-parallel low-angle or horizontal shear planes as displacement discontinuity as a function of coefficient of friction along them. The orientation of the largest principal stresses vary from diagonal (a) to high-angle (c and e), and finally sub-parallel (d, f) to the shear planes. From Ohlmacher and Aydin (1997).

Figure 2(a) shows a set of thrust faults along bedding planes or weak lithologies and small scale discontinuities such as veins and pressure solutions between them. 2(b) envisions these thrust faults cutting up-section to increase their length and 2(c) depicts larger scale interaction between sub-parallel large thrust faults and shear planes between them. Other related data and concepts are provided under 'Multiple Thrust Fault Sets.'

Figure 2. Conceptual models of a set of bed-parallel thrust faults and the related veins and pressure solution seams (a), lengthening of the system by cutting up-section (b), and more complex deformation between sub-parallel larger thrust faults commonly along weak horizons (c). From Ohlmacher and Aydin (1997).