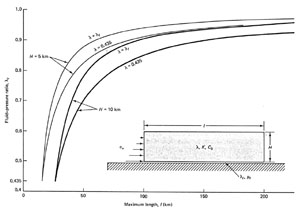
Modification to Anderson's faulting theory was made to deal with the potential impact of high fluid pressure that exists in Earth's crust and the associated effective stresses. Hubbert and Rubey (1959) first pointed out that effective normal stress should equal the normal stress minus the fluid pressure; this concept has enormous implication on frictional strength of faults, geometry of low angle faults, and size of thrust sheets.

Suppe (1985) reported that abnormally high fluid pressure ratio, in the range of 0.5 to 0.9, is quite common in many basins based on borehole measurements. Fluid pressure ratio is defined as the fluid pressure over overburden pressure. The normal range of this ratio is considered to be between 0.37 to 0.47. Suppe further discussed that when the fluid pressure ratio approaches 1, the fluid pressure approaches the magnitude of the overburden pressure. In this case, the shear strength of the fault is reduced to the cohensional strength of the surface which is rather small. Therefore, it is rather easy to form hydraulic fractures and to move faults at low angle or over horizontal planes in environments with high abnormal fluid pressures.

This fluid pressure concept helped to resolve the long-standing paradox that had to do with moving large scale thrust sheets while avoiding catastrophic failures within the sheet. According to Suppe (1985), high fluid pressure not only reduces the fracture strength of the fault plane, but also that of the overlaying thrust sheet. Suppe considered two categories of thrust sheet configurations. In one case, the fluid pressure ratio on the fault, lambda f, and within the overlaying block, lambda, are equal. This case represents a conservative estimate of the effect of fluid pressure on thrust faulting because it represents a maximum weakness within the thrust sheet. In the second case, fluid pressure ratio within the block is hydrostatic, 0.435, while the fluid pressure ratio along the fault elevates. The second case is an estimate of the maximum effect of fluid pressure on thrust faulting, because it maximizes the strength of the thrust sheet by having a low fluid pressure ratio within the block while minimizing the frictional resistance by having a high fluid pressure ratio along the fault. The geological situation corresponding to this case would be a thrust sheet in which the thrust sheet with the thrust fault is localized along the base of the fluid pressure transition zone, thereby maximizing the strength of the thrust sheet and minimizing the frictional resistance of the fault.

Suppe's results (Figure 1) showed in theory that it is possible to move long and thick thrust sheets along low-angle decollement planes if the fluid pressure ratio on the fault is large. Compared to a normal fluid pressure ratio of 0.435, a high ratio of 0.8 increases the maximum length of a 5 km thick thrust sheet from 20 km to over 40 km. For the same fluid pressure ratio increase, a 10 km thick thrust sheet can have lengths from 25 km to 50 km for the conservative estimation and to 70 km for the maximum estimation.

Figure 1. Maximum length of a rectangular thrust sheet that can be pushed across a horizontal decollement without fracturing within the sheet, as a function of fluid-pressure ratio along the fault. Two end-member fluid-pressure distributions are considered. The weak case has the same fluid-pressure ratio within the block as that along the fault. The strong case has a fixed hydrostatic pressure, 0.435, within the block, regardless of the fluid pressure on the fault. From Suppe 1985.