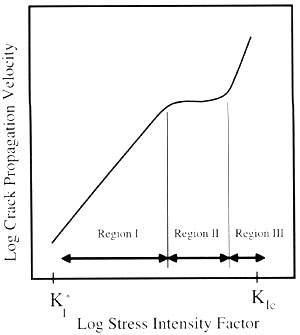
As pointed out in the section Joint Propagation Velocity affected by Stress Intensity, three regions in the plot of propagation velocity vs. stress intensity (Figure 1) are recognized. Subcritical propagation refers to the stage in which fractures propagate below the critical toughness, commonly called region I.

Figure 1. A schematic log-log plot of crack propagation velocity vs crack tip stress intensity factor showing three regions of crack growth. KI 'star' is the minimum stress intensity factor below which there is no propagation. KIC is the fracture toughness of a material, at which propagation becomes unstable. Crack propagation under KIC, if it occurs, is rather slow and stable. From Olson (2004).

The importance of subcritical growth for geological situations is that it is a stable propagation mechanism, in which the propagation velocity, v, is related to the opening-mode stress intensity factor at the crack tip, K(I), with an empirically quantifiable, power-law relationship (Equation 1). In Equation 1, K(IC) is the critical mode-I (opening mode) fracture toughness, n is the subcritical index and A is proportionality constant. The power-law exponent, n, can vary widely depending on rock type and environmental conditions (such as dry vs. wet). The higher the value of the subcritical index, the less important subcritical growth becomes, as very little propagation occurs before the fracture toughness is reached. For a given rock type, the subcritical index typically decreases with increasing water content in the environment. Reported values vary from 20 or less for tests carried out on sandstone submerged in water to greater than 250 under dry conditions in carbonate. Work in clastic sedimentary rocks suggests that grain size, grain mineralogy, cement type and porosity can influence the value of the subcritical index for a given environmental condition.

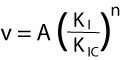Equation 1. Propagation velocity (v) as expressed by subcritical index (n), stress intensity factor (KI), as well as fracture toughness (KIC). A is a constant. From Olson (2004).